
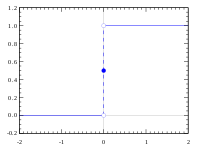
 The graph of the cubic function on the interval is closed because the function is continuous. The graph of the Heaviside function on is not closed, because the function is not continuous.
The graph of the cubic function on the interval is closed because the function is continuous. The graph of the Heaviside function on is not closed, because the function is not continuous.
In mathematics, the closed graph theorem may refer to one of several basic results characterizing continuous functions in terms of their graphs. Each gives conditions when functions with closed graphs are necessarily continuous.
A blog post by T. Tao lists several closed graph theorems throughout mathematics.
Graphs and maps with closed graphs
Main article: Closed graphIf is a map between topological spaces then the graph of is the set or equivalently, It is said that the graph of is closed if is a closed subset of (with the product topology).
Any continuous function into a Hausdorff space has a closed graph (see § Closed graph theorem in point-set topology)
Any linear map, between two topological vector spaces whose topologies are (Cauchy) complete with respect to translation invariant metrics, and if in addition (1a) is sequentially continuous in the sense of the product topology, then the map is continuous and its graph, Gr L, is necessarily closed. Conversely, if is such a linear map with, in place of (1a), the graph of is (1b) known to be closed in the Cartesian product space , then is continuous and therefore necessarily sequentially continuous.
Examples of continuous maps that do not have a closed graph
If is any space then the identity map is continuous but its graph, which is the diagonal , is closed in if and only if is Hausdorff. In particular, if is not Hausdorff then is continuous but does not have a closed graph.
Let denote the real numbers with the usual Euclidean topology and let denote with the indiscrete topology (where note that is not Hausdorff and that every function valued in is continuous). Let be defined by and for all . Then is continuous but its graph is not closed in .
Closed graph theorem in point-set topology
In point-set topology, the closed graph theorem states the following:
Closed graph theorem — If is a map from a topological space into a Hausdorff space then the graph of is closed if is continuous. The converse is true when is compact. (Note that compactness and Hausdorffness do not imply each other.)
ProofFirst part: just note that the graph of is the same as the pre-image where is the diagonal in .
Second part:
For any open , we check is open. So take any , we construct some open neighborhood of , such that .
Since the graph of is closed, for every point on the "vertical line at x", with , draw an open rectangle disjoint from the graph of . These open rectangles, when projected to the y-axis, cover the y-axis except at , so add one more set .
Naively attempting to take would construct a set containing , but it is not guaranteed to be open, so we use compactness here.
Since is compact, we can take a finite open covering of as .
Now take . It is an open neighborhood of , since it is merely a finite intersection. We claim this is the open neighborhood of that we want.
Suppose not, then there is some unruly such that , then that would imply for some by open covering, but then , a contradiction since it is supposed to be disjoint from the graph of .
If X, Y are compact Hausdorff spaces, then the theorem can also be deduced from the open mapping theorem for such spaces; see § Relation to the open mapping theorem.
Non-Hausdorff spaces are rarely seen, but non-compact spaces are common. An example of non-compact is the real line, which allows the discontinuous function with closed graph .
Also, closed linear operators in functional analysis (linear operators with closed graphs) are typically not continuous.
For set-valued functions
Closed graph theorem for set-valued functions — For a Hausdorff compact range space , a set-valued function has a closed graph if and only if it is upper hemicontinuous and F(x) is a closed set for all .
In functional analysis
Main article: Closed graph theorem (functional analysis)If is a linear operator between topological vector spaces (TVSs) then we say that is a closed operator if the graph of is closed in when is endowed with the product topology.
The closed graph theorem is an important result in functional analysis that guarantees that a closed linear operator is continuous under certain conditions. The original result has been generalized many times. A well known version of the closed graph theorems is the following.
Theorem — A linear map between two F-spaces (e.g. Banach spaces) is continuous if and only if its graph is closed.
The theorem is a consequence of the open mapping theorem; see § Relation to the open mapping theorem below (conversely, the open mapping theorem in turn can be deduced from the closed graph theorem).
Relation to the open mapping theorem
Often, the closed graph theorems are obtained as corollaries of the open mapping theorems in the following way. Let be any map. Then it factors as
- .
Now, is the inverse of the projection . So, if the open mapping theorem holds for ; i.e., is an open mapping, then is continuous and then is continuous (as the composition of continuous maps).
For example, the above argument applies if is a linear operator between Banach spaces with closed graph, or if is a map with closed graph between compact Hausdorff spaces.
See also
- Almost open linear map – Map that satisfies a condition similar to that of being an open map.Pages displaying short descriptions of redirect targets
- Barrelled space – Type of topological vector space
- Closed graph – Graph of a map closed in the product spacePages displaying short descriptions of redirect targets
- Closed linear operator
- Discontinuous linear map
- Kakutani fixed-point theorem – Fixed-point theorem for set-valued functions
- Open mapping theorem (functional analysis) – Condition for a linear operator to be open
- Ursescu theorem – Generalization of closed graph, open mapping, and uniform boundedness theorem
- Webbed space – Space where open mapping and closed graph theorems hold
- Zariski's main theorem – Theorem of algebraic geometry and commutative algebra
Notes
References
- ^ "The closed graph theorem in various categories". 21 November 2012.
- Rudin 1991, p. 51-52.
- Rudin 1991, p. 50.
- Narici & Beckenstein 2011, pp. 459–483.
- Munkres 2000, pp. 163–172.
- Aliprantis, Charlambos; Kim C. Border (1999). "Chapter 17". Infinite Dimensional Analysis: A Hitchhiker's Guide (3rd ed.). Springer.
- Schaefer & Wolff 1999, p. 78.
- Trèves (2006), p. 173
- Noll, Dominikus (2024). "Topological spaces satisfying a closed graph theorem". arXiv:2403.03904 .
Bibliography
- Bourbaki, Nicolas (1987) . Topological Vector Spaces: Chapters 1–5. Éléments de mathématique. Translated by Eggleston, H.G.; Madan, S. Berlin New York: Springer-Verlag. ISBN 3-540-13627-4. OCLC 17499190.
- Folland, Gerald B. (1984), Real Analysis: Modern Techniques and Their Applications (1st ed.), John Wiley & Sons, ISBN 978-0-471-80958-6
- Jarchow, Hans (1981). Locally convex spaces. Stuttgart: B.G. Teubner. ISBN 978-3-519-02224-4. OCLC 8210342.
- Köthe, Gottfried (1983) . Topological Vector Spaces I. Grundlehren der mathematischen Wissenschaften. Vol. 159. Translated by Garling, D.J.H. New York: Springer Science & Business Media. ISBN 978-3-642-64988-2. MR 0248498. OCLC 840293704.
- Munkres, James R. (2000). Topology (2nd ed.). Upper Saddle River, NJ: Prentice Hall, Inc. ISBN 978-0-13-181629-9. OCLC 42683260.
- Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
- Rudin, Walter (1991). Functional Analysis. International Series in Pure and Applied Mathematics. Vol. 8 (Second ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 978-0-07-054236-5. OCLC 21163277.
- Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
- Trèves, François (2006) . Topological Vector Spaces, Distributions and Kernels. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-45352-1. OCLC 853623322.
- Wilansky, Albert (2013). Modern Methods in Topological Vector Spaces. Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-49353-4. OCLC 849801114.
- Zălinescu, Constantin (30 July 2002). Convex Analysis in General Vector Spaces. River Edge, N.J. London: World Scientific Publishing. ISBN 978-981-4488-15-0. MR 1921556. OCLC 285163112 – via Internet Archive.
- "Proof of closed graph theorem". PlanetMath.
| Functional analysis (topics – glossary) | |||||
|---|---|---|---|---|---|
| Spaces |
| ||||
| Theorems | |||||
| Operators | |||||
| Algebras | |||||
| Open problems | |||||
| Applications | |||||
| Advanced topics | |||||
| Topological vector spaces (TVSs) | |
|---|---|
| Basic concepts | |
| Main results | |
| Maps | |
| Types of sets | |
| Set operations | |
| Types of TVSs |
|
 on the interval
on the interval  is closed because the function is
is closed because the function is  is not closed, because the function is not continuous.
is not closed, because the function is not continuous.
 is a map between
is a map between  is the set
is the set  or equivalently,
or equivalently,
 It is said that the graph of
It is said that the graph of  is a
is a  (with the
(with the  between two topological vector spaces whose topologies are (Cauchy) complete with respect to translation invariant metrics, and if in addition (1a)
between two topological vector spaces whose topologies are (Cauchy) complete with respect to translation invariant metrics, and if in addition (1a)  is sequentially continuous in the sense of the product topology, then the map
is sequentially continuous in the sense of the product topology, then the map  is any space then the identity map
is any space then the identity map  is continuous but its graph, which is the diagonal
is continuous but its graph, which is the diagonal  , is closed in
, is closed in  if and only if
if and only if  with the usual
with the usual  denote
denote  and
and  for all
for all  . Then
. Then  then the graph of
then the graph of  where
where  is the diagonal in
is the diagonal in  .
.
 , we check
, we check  is open. So take any
is open. So take any  , we construct some open neighborhood
, we construct some open neighborhood  of
of  , such that
, such that  .
.
 on the "vertical line at x", with
on the "vertical line at x", with  , draw an open rectangle
, draw an open rectangle  disjoint from the graph of
disjoint from the graph of  , so add one more set
, so add one more set  .
.
 would construct a set containing
would construct a set containing  .
.
 . It is an open neighborhood of
. It is an open neighborhood of  such that
such that  , then that would imply
, then that would imply  for some
for some  by open covering, but then
by open covering, but then  , a contradiction since it is supposed to be disjoint from the graph of
, a contradiction since it is supposed to be disjoint from the graph of  .
.
 has a closed graph if and only if it is
has a closed graph if and only if it is  .
.
 is a linear operator between
is a linear operator between  is a
is a  .
. . So, if the open mapping theorem holds for
. So, if the open mapping theorem holds for  ; i.e.,
; i.e.,